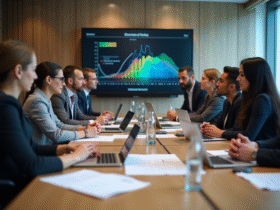
Le prix d’une option d’achat, ou ‘call’, peut être influencé par divers facteurs. Parmi eux, le taux d’intérêt joue un rôle souvent sous-estimé mais fondamental. Lorsque les taux d’intérêt augmentent, la valeur d’un call tend à croître. Cette relation s’explique par le coût de portage, qui rend l’investissement plus attractif à mesure que les taux montent.
À l’inverse, une baisse des taux d’intérêt peut réduire l’attrait des options d’achat. Les investisseurs doivent donc surveiller de près les mouvements de taux pour optimiser leurs stratégies. Comprendre ces dynamiques permet de mieux naviguer dans l’univers complexe des produits dérivés.
A lire également : Les meilleures compagnies d'assurance : sélection et critères d'évaluation
Plan de l'article
Les taux d’intérêt et leur influence sur les options financières
Les taux d’intérêt jouent un rôle déterminant dans l’économie et, par extension, sur le prix des options. Les banques centrales modulent les taux directeurs pour contrôler la dynamique économique globale. Ces ajustements influencent directement les taux d’intérêt du marché, affectant ainsi le coût d’opportunité du capital investi.
Impact des taux d’intérêt sur les options
Les fluctuations des taux d’intérêt influencent le prix des options de plusieurs manières :
A lire également : Comparatif des meilleures assurances auto disponibles
- Une hausse des taux d’intérêt augmente le coût de portage, ce qui rend les options d’achat plus attractives.
- À l’inverse, une baisse des taux peut réduire leur attrait en diminuant le coût d’opportunité.
Rôle des banques centrales
Les banques centrales ajustent les taux directeurs pour réguler l’économie. Ces ajustements se répercutent sur les taux d’intérêt du marché, affectant ainsi les décisions d’investissement dans les options. Un environnement de taux élevés favorise généralement les positions longues sur call, tandis qu’un environnement de taux bas peut inciter à la prudence.
| Facteur | Impact sur le prix du call |
|---|---|
| Taux d’intérêt en hausse | Augmentation du prix du call |
| Taux d’intérêt en baisse | Diminution du prix du call |
Modèle Black-Scholes et taux d’intérêt
Le modèle Black-Scholes est couramment utilisé pour évaluer les options. Ce modèle intègre plusieurs paramètres, dont le taux sans risque, la volatilité, le prix spot, le prix d’exercice et la maturité. Parmi les ‘Grecs’, le Rho mesure la sensibilité du prix de l’option aux variations des taux d’intérêt. Une compréhension fine de ces interactions permet d’optimiser les stratégies de trading et de gestion de portefeuille.
Impact du taux d’intérêt sur le prix d’un call
Les taux d’intérêt influencent directement le prix des options d’achat, ou calls. Le modèle Black-Scholes, couramment utilisé pour évaluer les options, intègre le taux sans risque comme un paramètre fondamental. Effectivement, une augmentation du taux d’intérêt entraîne généralement une hausse du prix du call. Cette relation s’explique par le coût de portage des actifs sous-jacents, qui devient plus élevé lorsque les taux augmentent.
Dans ce contexte, le Rho, l’une des « Grecs » utilisées pour mesurer la sensibilité des options, devient particulièrement pertinent. Le Rho quantifie l’impact des variations de taux d’intérêt sur le prix de l’option. Un Rho positif signifie qu’une hausse des taux d’intérêt augmente la valeur de l’option d’achat.
Considérez les éléments suivants pour mieux comprendre cette dynamique :
- Une hausse des taux d’intérêt augmente le coût de portage, rendant les options d’achat plus attractives.
- À l’inverse, une baisse des taux diminue ce coût, réduisant l’attrait des calls.
Le modèle Black-Scholes prend aussi en compte la volatilité, le prix spot, le prix d’exercice et la maturité. Tous ces paramètres sont interconnectés et influencent le prix final de l’option. En particulier, la volatilité amplifie les chances que l’option finisse dans la monnaie, augmentant ainsi la valeur potentielle du call.
Les acteurs du marché doivent donc suivre attentivement les décisions des banques centrales et les variations des taux d’intérêt pour optimiser leurs stratégies de trading d’options. La compréhension des interactions complexes entre ces paramètres et l’utilisation correcte des Grecs permettent une gestion plus fine et précise des portefeuilles d’options.
Facteurs clés influençant la variation du prix d’un call
Les options financières sont influencées par plusieurs facteurs interconnectés, connus sous le nom de « Grecs ». Ces paramètres permettent de mesurer la sensibilité du prix des options à différents éléments du marché.
Delta mesure la variation du prix de l’option par rapport à une variation du prix spot de l’actif sous-jacent. Plus le Delta est élevé, plus le prix de l’option est sensible aux mouvements de l’actif sous-jacent.
Gamma quantifie la sensibilité du Delta. Un Gamma élevé indique que le Delta changera rapidement en réponse aux variations du prix de l’actif sous-jacent.
Vega mesure la sensibilité du prix de l’option à la volatilité de l’actif sous-jacent. Une volatilité élevée augmente la valeur potentielle du call, car elle amplifie les chances que l’option finisse dans la monnaie.
Thêta évalue l’impact du temps sur le prix de l’option. À mesure que la date d’expiration approche, la valeur temporelle de l’option diminue, ce qui peut éroder le prix du call.
| Grecque | Description |
|---|---|
| Delta | Variation du prix de l’option par rapport au prix spot |
| Gamma | Sensibilité du Delta |
| Vega | Sensibilité à la volatilité |
| Thêta | Impact du temps sur le prix |
La volatilité reste un facteur central. Elle influence directement les chances que l’option termine dans la monnaie. Une volatilité implicite élevée rend les options plus chères, reflétant l’incertitude du marché.
Suivez aussi les décisions des banques centrales, qui modulent les taux directeurs et influencent ainsi directement le coût d’opportunité du capital investi. Les variations des taux d’intérêt se répercutent sur le prix des calls, rendant fondamental le suivi de ces indicateurs pour une gestion optimisée des portefeuilles d’options.